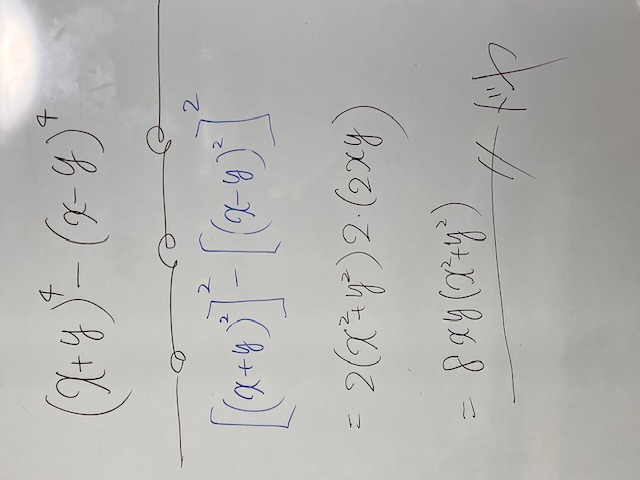数１A

数１A · 07日 4月 2025

2次方程式の解の公式は、新高1の皆さん覚えてますよね。この解の公式を自分で証明できるように練習しといてください。中3の教科書に載ってます。因数分解の公式③番を使うやつです。高校に入ったらこの平方完成を暗算で解いていきます。もしかして、新高1の数学の授業で出されるかもしれませんよ。（過去に某道立高で出題されました）ついでに、偶数編にも挑戦してみてください。解けたら、今後は安心して偶数編使えますね。実は、この解の公式は死ぬほど出てくるんです。特に2次関数のグラフを書くと言ったら判別式ですからね。高校数学最初の授業の日まで、解の公式を証明できるようにマスターしとけばいいことあるかもです。おまけでした。

数１A · 02日 4月 2025

中3生、今は輪環の順で答えるようになりました。最終仕上げとして、今年の卒塾生が寄付してくれた青チャートのEXERCISESより数問出題しました。←は青チャートでは④入試の基本～標準レベルとされてます。本問をスラスラ解ける生徒さんは、問題ありません。このまま勉強を続けていってください。どんどん力がつくでしょう。中3のみなさん、高校数学・予習シリーズお疲れさまでした。演習問題ができたできなかったは別にして、高校数学がどんな世界なのかを少し垣間見れただけでもアドバンテージになります。心構えが全然違うはず。この先、数学で学年上位を目指してください。ちゃんと復習すれば、成れるはずです。今回は、それだけの良問をこなしましたので、入学式の日までガンガン復習し続けて自信をつけてください。素晴らしいスタートダッシュが決まるでしょう！…以下、塾を探してる高校生、保護者の皆さまへ。当塾の高校数学クラス（一人～三人）は、このような問題、つまり基礎～入試標準～やや難レベルまでを、生徒さん一人一人に合わせて演習していきます。初学者でも大丈夫です。

数１A · 31日 3月 2025

この問題を中3に出題しました。制限時間は2分です。つまり、2分以内で解けるんだよ、という優しいHINTなのです。言い換えると、習ったことで解けますよ、という意味です。当塾では、未履修部分は出題しません。当たり前ですが、習ったこと、学んだことを利用して解ける問題しか出しません。黒で書かれた4乗-4乗の因数分解しなさい、です。因数分解しなさい、ということは、因数分解できますよ、ということですよね。どう見ても、公式4番風じゃないですか。これ以外に何が思いつきます？笑。複二次式（授業で、この名前を教えました）風で2乗ひく2乗 このように（←図）3行で仕留めてドヤ顔しましょう。こんな解答した生徒には、もし私が高校の先生なら、105点あげるでしょう。是非、使いこなせるようになってください。

数１A · 26日 3月 2025

(1)は、全員解けました。力業でも何でもいいんです。その子にとって最速で、かつ確実に正確に辿り着けるのであれば、今は贅沢言いません。ですので(1)は解けて当然です。ですが・・・なんと(2)と(3)が解けませんでした。私が問題視するのは、(2)が解けなかった事です。生徒たちはできないかもと覚悟はしてましたが、嫌な予感は的中。実は(2)は3/18のblog予習⑥と同問なのです。当初はa,b,cに変えようかと思いましたが、優しい親心で文字を変えずにそのまま出題しました。なんと復習してないのがバレましたね。実際は、こんなもんです苦笑。勉強すればできる、数学が得意な子達でも、復習しないから忘れる。あぁ～ぁ、もったいない。もし、国公立・有名私大を目指すならやるべきです。(3)の手順を示したら前回同様、生徒たちからは「あぁっ」悔しそうな溜息がもれました。そうだよ、今からでも遅くないです。しっかり復習しましょう。君たちは、やればできる子なんだから。自分の可能性を摘まないで、大いに伸ばしてください。期待してます。

数１A · 24日 3月 2025

塾の中3が解けるかどうか、フォーカス　ゴールド　数Ⅰの問題（＊＊）を出してみました。私としては練5の(4)以外は、全問正解して欲しかったのですが、7問できたのは1人だけでした。そして全員(4)が解けなかった。中3には難しく見えるのかな。んなことないのに。私は、さらっと全問解法の手順を示しました。さらっと・・・つまり、詳しく解説する必要はありません。授業で何回も触れてる部分ですので、今更不要ですから。手順を見た生徒たちからは「あぁ～、そうだった」とため息が漏れます。「でしょ。何度もやったよね。順瞬殺レベルでしょ。でも、なぜ解けなかったと思う？あんたたち、復習してないからだよね。悔しいね、残念でしょ。はい、今から復習やる！（やれ）」数分間の復習タイムを与えます。「予習してるあなた達でもまだ解けないんだよ。春休みに高校数学の準備無しの新高1は、あなた達よりもっと解けない、悲惨な結果になるのわかるでしょ」。このショックな結果で、復習の重要性を真摯に受け止めてくれたら幸いです。大学入試の難易度は地元公立高校入試の比じゃないですからね。自分以上のライバルが全国から集まってくるんだよ。勝てる？

数１A · 18日 3月 2025

さて、どうしましょうか。よく見るとX→Y→2Z→Xと循環してるのでパターンに嵌めれそうですが、符号が変わったりしてる部分もあるので難しそうだから却下。また、1次のものが3つ入った3乗を力業で展開しても項数二桁と多くなり、ノートに横一列に書ききれない。この案も没。なら、工夫するしかないですね。私達は「和の2乗と差の2乗の和や差」を見つけたらラッキー、楽勝で即暗算でした。つまり、それを真似て「3乗」でも似たような方法作れるかどうか実験してみましょう。←図、緑線②、青線③の部分です。出来ちゃいましたね。では早速これらを利用。結果、数行で終わり、ラク出来ちゃいました。しかも、赤線④見た瞬間、生徒達は顔がにやけたはず。ここにもいたのか、ってね。さり気にやってますが、本問も大学入試の過去問です。これで、数Ⅰは展開まで終了。復習しといてください。次回の授業では、Focus Goldから練習問題を3問、中3に出題してみます。さて、何割正解できるかな？ 中3に大学入試レベルですが、うちの中3なら、正直全問正解もあり得ます。そしたら嬉しいな。ちょっぴり期待しちゃいます。復習しててね、してる・・・よね？

数１A · 16日 3月 2025

高校数学準備編2日目は、前回の復習から入り、本日は←図の問題をやりました。本問をよく見ると、一次のものが3つ入ったカッコが4個の掛け算になってます。はぁ？こんなのを一気に展開する公式なんか教科書に載ってません・汗。でも、展開せよと出題されてるということは、いいですか、「工夫したら解けますよ」ということです。私たちが教科書等で習ってるのはカッコの中身が2個の展開が多いので、見慣れたその2個風に変形してみましょう。←2行目。とりあえずaを含む、含まない、に分けてみました。これだと見慣れた型なので、今後の展開は上手くいきそうな予感がしますね。なら、その予感を信じて迷わずそのまま計算しちゃいましょう。ダメだったら諦めて、やり直せばいいんですから。あれれ、結果意外と簡単に解けちゃいましたね。振り返ってみれば、意外と簡単でした。勇気をもって挑んだら私でも解けちゃった、嬉しい！このように、今の自分が持ってる力だけで解けることが結構あります。だめで元々、すぐには諦めず、少しだけでも工夫してみましょう。どんな人でも、やればできるようになります。当塾では、生徒の性格に合わせて、ヒントを与えてます。

数１A · 15日 3月 2025

先日の問題の別解・エレガント編です。要は、工夫すると計算が楽になる場合がある例です。もし、知識としてストックできるなら、覚えておくと試験で計算時間を短縮できライバルに差をつけられます。いいですか。さらっと言いましたが「復習するんだよ。せぇよ。」の意味ですからねwww。これくらいこなす高1ザラにいますから。真剣に受け止めて復習してくるか、あるいはまだ聞き流してるだけなのか、今後の演習で判明するでしょう。3/4の公立高校入試が終わった日から当塾の中3の授業は高校数学・予習が始まり、開始1日目でここまで進みました。途中の練習問題は中3レベルなので、授業ではすっ飛ばし宿題にしました。いよいよ次回からは、高校の因数分解が牙をむいてきます。どんどん難しくなります。難問までとり扱います。ここをしのげれば、高校数学スタートに自信が持てます。とにかく、最初の因数分解でくじけないように頑張ってください。私のイメージでは・・・高校の数学は中学のに比べ、10～15倍は難しくなると思います。いや、もっとかも。この子達も、徐々に実感するでしょう。早く気が付いた方が勝ちですよ。

数１A · 12日 3月 2025

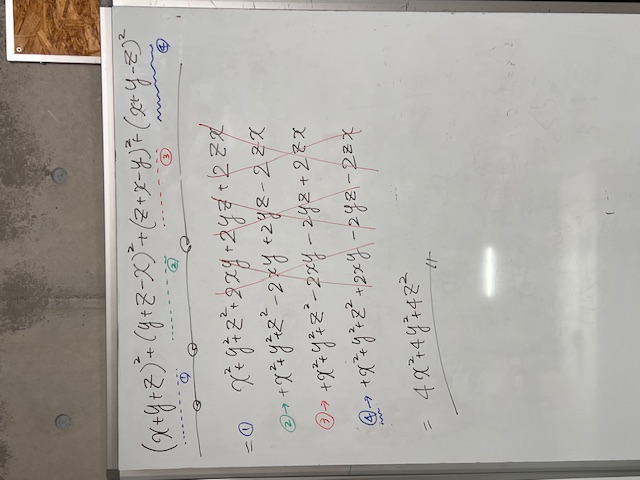
一見複雑そうに見えますが、実はこの問題は結構簡単なんです。2乗の( x + y + z )^2の公式を使い、ただひたすらに力業で展開すれば必ず解けます。ただしコツは、←図のように、各項を上下に揃えて書くと見やすくなり、ミスが激減します。揃えないで、そのままだらだら横に書いていくと・・・やってみてください。異常に時間かかり手が止まるでしょう。今回のは、最初に書きましたが( x + y + z )^2（←2乗の意味です）の公式を知ってることが前提になりますので、まだの人は今スグ覚えてください。教科書に載ってるはずです。次回は、同問題をもっと少ない手数で解く別解です。 塾の生徒には伝えてます。次回やる方法を知っているといいことがある。ライバルに差をつけられるから、頑張って習得した方がいい。やる、やらないは貴方次第。復習して身につけておけば、いつか難問で必ずあなたを助けてくれるはず。 この春休み中に、どれだけ高校数学の予習をしておくか。やればやるほど成績上がります。保障します。それ程スタート前の準備が、超大事です。逆にやらないでいると、大きく出遅れるかも。落ちこぼれる可能性さえあります。

数１A · 08日 3月 2025

与式を落ち着いて、じっくり眺めてみましょう。1次式4個の積なので、普通は相性が良い2個ずつを選び1セットにして、できた2セットを順番に展開して解くと思います。←画像の上から2行目～5行目。これの別解（下段）：「暗算で解く」練習も、してみてください。考え方は、与式は、1次のものが4個並んだ積（かけ算）だから、どうせ出てくるのは4次のものですよね。じゃぁ、各項の係数は、その都度残り物の組み合わせで考えれば出せそうだ、と考えます。全部で16パターンを計算。こうやって←画像を見ると、暗算がちょっと難しければ、ちょこっと計算メモしながら、暗算風に解く、でも全然OK。それでも、断然速いはず。いきなり、最下段の答えをズバッと書いたら、周りのお友達はビックリするはず。尊敬されること間違いなし。なら、ちょっと頑張って練習してみましょう。実はこれ、当塾の中3の問題集にも出てます。中学生には、上の、2セットにしてから展開する方法で解かせてます。でも、高校生になったら、できる範囲で項毎に計算する癖をつけてください。