中2
中2 · 09日 2月 2025
中2が単元テストで100点を取りました(祝)。たとえ単元テストでも、100点は嬉しいものです。期末や実力テストでの100点は無理ゲー、到底届く筈もない夢の夢。そんな子らにとって、単元テストで100点という結果は大きな自信になったでしょう。It is always rewarding to study hard. 2月に入り、間もなく殆どの試験が終わろうとしてます。今の時期から4月の新学期が始まるまでの期間に、どれだけ苦手科目を克服できるかが勝負。今の中2にとって、この春の過ごし方が来年の高校入試に大きな影響を与えるでしょう。彼らにとって5教科全部を自分一人で復習は無理。できるのならとっくにやってて、もっとテストの点数が良いはずですよねwww。そこで私は、この春迄に取り組むべき教科1~3つを全員の前で個別に与えました。(与えてない子もいます)その都度歓声が上がったり、苦悶の表情を見せる等様々でまるでエンタメショー。でも、逃げてたら始まりません。この春は挑んでもらいます。頑張れば、必ず報われる。It is always rewarding to study hard.
中2 · 14日 1月 2025
各学年とも、comfort モードは4~5名です。先日、中2クラスの数学の時間で指数法則に触れた時、皆悩み苦しみながも、指数法則の意味を自分の力で解けた喜びから「楽しい」という歓声まであがり、大変盛り上がりました。当塾の中2生全員数学が得意、ということは決してありません。寧ろ、平均点以下からスタートした生徒が殆どです。こんな中2クラスですが、先日も連立方程式のプリントを解くのが以前とは比べ物にならないくらい、普通の速さなってましたwww。しかも全員同じペースでペンが進んでた事にも驚きました。この一ヶ月間で中2生は2名増え、現在5名になりcomfortableですが、もし、自分も大島学習塾に入って頑張りたいという強い意志があれば、あと、MAX2名までは新規塾生受け入れ可能です。学校の数学のテストで、今は平均点前後だけど、これからは平均点以上になりたい。または、平均点よりもっと上の、平均点+30点くらいまでを目指したい生徒さんに最適なクラスです。自分一人では勉強できないけど、周りにつられてなら勉強できる、これからは部活も勉強も頑張ってみたい。そんな中2生をあと2名までお待ちしております。
中2 · 13日 6月 2024
数学は平均点以下からスタートし、今は平均点+20くらいは取れるようになってきたある生徒さんの計算の展開の様子を見ると、同類項があった時はそいつらを一緒に並べて書いてました。「凄いね君。いきなりこんな風に書くなんて。もしできるのなら、このやり方とってもいいよ」「私、いつもこれでやってます」「じゃぁ、この問題を暗算でやってみようか。君ならできるかもしれないよ」私は青チャートの数1Aを取り出し、画像の(3)をさせてみました。参考書の(3)の模範解答の2列分をすっ飛ばし、いきなり3列目と同じ計算を、しかも暗算でさせます。ちなみにこれは高校1年生の問題で、当塾の高1クラスではこの手の問題は、出来るだけ暗算で解かせてます。「まずX^2の係数だけね。Aのは-3倍して、Bのを2倍して加えて、そしてCのを引くんだよ・・・いくつになる?」「-4xの2乗」。「あってる!」本人、楽しかったのか「先生、この問題コピーしてもらってもいいですか。家でもやってみたいんです」。家での復習が楽しみになる。こんなことあります?
中2 · 08日 6月 2024
予感どうり、中2生の爆上げ3人目が出ました。今度は数学で、92点(平均点55点)。この生徒も前々回の定期テストでは52点、前回の実テでも55点。今回は単元テストですが、それでも92点は立派です。間違えた2問も空欄ではなく、チャレンジした結果のミスなので咎めません。昨日しっかり塾で復習したので次回正解出来れば良いのです。中2生の3人とも、90点以上をとってきて全員が拍手(祝福)されたことになります。一人だけが爆上げしたではありません。また一人だけ、伸びなかったのでもありません。3人とも同時に爆上げしたのです。こんなことってありますか?決して塾の自慢ではありません。3人とも、まじめに授業に取り組んでくれたおかげです。塾では、これでもかというくらい繰り返しやります。それでも正直、テストでは間違えます。そんなもんです。塾では出来るようになったけど、学校でのテスト本番では緊張して実力発揮できない。自宅での練習不足なだけです。これを繰り返し行っていけば、いずれ良い点数を取れるようになります。まだまだ始まったばかりの中2クラス、これからも楽しみです。
中2 · 06日 6月 2024
私の予感通り、中2生の爆上がりが始まってます。二人目が出ました。彼女が塾に持参してくれた解答用紙に並んだ3桁の数字が私の目に飛び込んできました。100点です。確かにこの生徒は、塾の授業中の先生(私)からの出題に、ほぼ全問口頭でちゃんと答えてましたので、かなり良い点数取ってくるだろうなという予測はありましたが、満点だなんて。おめでとう。本人、私だけでなく塾の生徒も一緒に喜び、拍手。学校のクラスメイトや先生、そして保護者様からは「凄すぎる」と称賛されたそうです。そりゃそうですよね。でも、私達にとっては、してやったりです。ちなみに、この生徒さん、前々回の定期テストで社会は28点(もちろん平均点以下)で、前回の実テでは46点でした。そして今回の単元テストではなんと100点。私たち以外では誰も想像しえなかったでしょうね。ちなっみに100点は学年で10人だけだそうです。彼女も爆上げ開始です。中2のこの快進撃、まだまだ続くのか?(続いて欲しい)
中2 · 30日 5月 2024
現中2クラスは、全員が平均点以下からスタートしたクラスですが、
私が予感してた爆上がりが徐々に始まりました。今の時期、各中学校で単元テストが行われてます。まず、一番苦手だった社会で、いきなり94点取ってきた子が現れました。この生徒も前回のテストではもちろん平均点以下です。隠さず言います、実テで22点でした。その子が94点!凄い!頑張りましたね。多分、担任の先生や保護者様は驚いたことでしょう。正直、私だって驚きましたもん。本人も嬉しかったでしょう。このように現中2クラスは、お互いが心地よい緊張感の中で全員が頑張ってます。いいぞ、みんなこの調子で理科も英語も克服しよう!
中2 · 14日 5月 2024
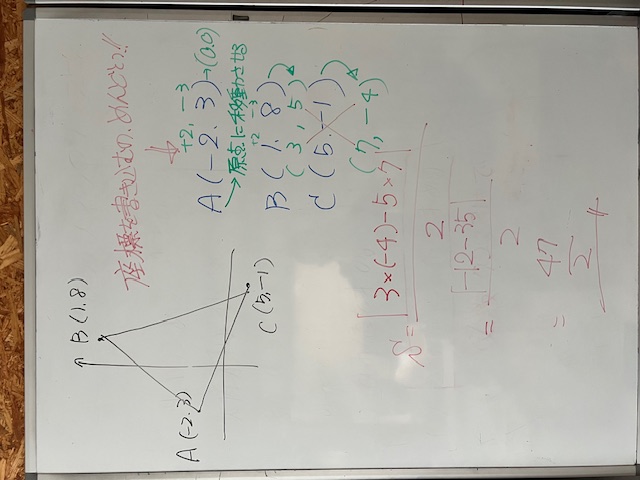
今回は、原点を頂点としない三角形の面積を求める問題です。どの頂点も原点にないから、必殺・クロス引きが使えません。原点を通らないから使えない。困った。使えるようにしたい。じゃぁ、どうすれば使えるようになるかな?どれか一つの頂点が原点になればいいんです。そっか、そうだよね。あはは。これに気が付いたら貴方は勝ち。この時点で80%は終わります。どれか一つの頂点を原点まで平行移動してあげたら、同様に他の2頂点も平行移動してあげればいいんです。今回は、点Aを原点に平行移動させました。同様にBもCも平行移動。そのあと、堂々と「必殺・クロス引き」しましょう。
中2 · 28日 4月 2024
このクラスが当塾で、一番成績が伸びてるクラスです。1年前の入学時、全員平均点以下からスタートしてます。それが平均点を超えはじめました。4月から1名増え、そのことによって心地よい緊張感が生まれてます。数学の学校ワークを全員が殆ど間違えなくなってるのです。あれほど計算苦手だった生徒も別人のように正解しまくり。多分中学校の先生、お友達も驚くはず。そんな予感がします。この調子で伸び続けて欲しいです。新中2の期末テストが今から楽しみになってきました。もしかして、とんでもない報告ができるかも。それくらい楽しみな中2クラスです。既塾生の先日4/19の実力テストの点数は、170~270点の範囲でした。塾を探してる中2で150点~290点だった生徒さんに超お薦めのクラスです。是非一緒に勉強頑張ってやってみましょう。
中2 · 23日 1月 2024
三角形の面積を二等分する直線の問題は、2パターンあります。① どこかの頂点を通る場合。これは、三角形の底辺の長さを半分にすれば高さは変わらないので面積は半分になるよね。なのでこのパターンは超簡単です。②頂点を通らない場合。こちらは厄介です。必殺の方法が無いので、まめに面積を計算していくしかありません。< (2)の解法 >まずは△ABCの面積を求めます。点Aを原点に移動させ、BもCも同様に平行移動させ、秘儀「クロスびき」で面積をサクッと求めます。面積は15。次に原点から辺BCに適当に線を引き、交点をDとします。この点Dの座標を決めてあげましょう。DのX座標は仮の姿のtにしときます。Y座標は、まだ決められません。直線BCの式を求め、それに代入して求めます。最後に、△ODCの面積の式をクロス引きで建て=15/2とおけば終わり。解くとtの値が求まります。※クロス引きは、高校のベクトルで習います。今は数Cになるのかな。でも、使い方は超簡単なので、中学生でもなんなく使いこなせます。速い生徒なら、この問題を3分くらいで解いちゃいますので、覚えたほうが徳です。
中2 · 10日 12月 2023
サイコロ2個の確率の時は、無条件に6x6の全事象(出目総数)分の表を作り、そこに出た目の積で4の倍数になる個所に印を書き込んであげればいいんですよね。ただし、ここで注意が必要です。先日、数検3級対策でこの問題をやった小6は、思いつくまま暗算しながら、いきなり表に印を書き込みました。で、結果、間違えてしまったのです。何がいけなかったのでしょうか。かけ算を思いつくまま書き込んだため、漏れが生じました。こういうミスを防ぐ為に、書き込む前に根元事象、つまり4の倍数になるかけ算の組み合わせを全部書き出しましょう。あとは、それを見ながら表に印を書き込めばいいんです。このやり方で解きなおした小6は、正解することができました。実は、このやり方を覚えちゃえば、6x6の表が無くても大丈夫ですね。気をつける点→同じ型のサイコロだけど、別々のサイコロ(イメージとして白と青の色違い等)として扱うんだよ。もし、(1,4)と(4,1)が同じものとして考えたなら、全事象数36も減って36じゃなくなる。つまり分母の数も変わってしまうよね。